PROPRIEDADES DAS PROGRESSÕES ARITMÉTICAS

1.a propriedade (termos eqüidistantes dos extremos)
Numa P.A. finita, de dois termos eqüidistantes dos extremos é igual à soma dos extremos.

Exemplo:

Seja a P. A. (8, 10, 12, 14, 16). Observa-se que:

Os termos a₂ = 10 e a₄ = 14 estão eqüidistantes dos extremos a₁ e a₅, respectivamente.

Note que: 10 + 14 = 8 +16 = 24 .

2.a propriedade

Numa P.A. com número ímpar de termos, o termo médio é igual à média aritmética entre os extremos. 

Exemplo:
Na P. A. (2, 4, 6, 8, 10), temos: 



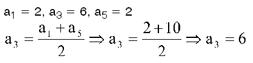
3.a propriedade
A seqüência (a, b, c) é P.A. se, e somente se, o termo médio é igual à média aritmética entre a e c, isto é:

Extraido de :

https://www.colegioweb.com.br/matematica/propriedades-das-progressoes-aritmeticas.html