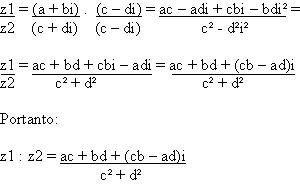Divisão de Números Complexos

CONJUGADO DE UM NÚMERO COMPLEXO

Dado um número complexo z = a + bi , chama-se conjugado de z e representa-se por , a um outro número complexo que possui a mesma parte real de z e a parte imaginária o simétrico aditivo da parte imaginária de z .

z = a + bi ® = a - bi
Ex: z = 3 + 5i ; = 3 - 5i

Obs : Sabemos que os números complexos podem também ser representados na forma de pares ordenados . Assim é que z = a + bi = (a,b).
Portanto , por analogia com o sistema de coordenadas cartesianas , pode-se representar graficamente qualquer número complexo z num sistema de coordenadas cartesianas , bastando marcar a parte real a no eixo horizontal e a parte imaginária b no eixo vertical . Neste caso , o eixo horizontal é chamado eixo real e o eixo vertical é chamado eixo imaginário. O plano cartesiano, neste caso , denomina-se plano de Argand-Gauss.
O ponto que representa o número complexo z , denomina-se afixo de z.

DIVISÃO DE NÚMEROS COMPLEXOS NA FORMA BINÔMIA

Regra : Para dividir um número complexo z por outro w ¹ 0 , basta multiplicar numerador e denominador pelo complexo conjugado do denominador .

Ex: = = = 0,8 + 0,1 i

De uma forma geral podemos demonstrar a divisão de dois números complexos por:

Dado z1 = a + bi e z2 = c + di a divisão de z1 : z2 será: